递归函数简单来说就是在一个函数体内调用了该函数自己。

递归的组成

• 递归调用（在函数里调用自身）
• 递归终止条件（也叫递归出口，如果没有递归出口，控制台会报错 RecursionError，超出最大递归深度）

只要能找到递归出口，递归就好写了。绝大多数的递归都可以用循环来实现。

使用递归最典型的就是计算阶乘和计算斐波那契数列这两个问题。

示例1：计算n！。

def fac(n):
    if n == 1:  # 递归出口
        return 1
    return n*fac(n-1)   # 递归调用函数自身

num = int(input('请输入一个整数：'))
# s = fac(num)
# print(s)
print(f'{num}！计算结果是{fac(num)}')


# 递归部分使用循环去写n！
def fac1(n):
    m = n
    for i in range(1,n):
        m *= i
    return m

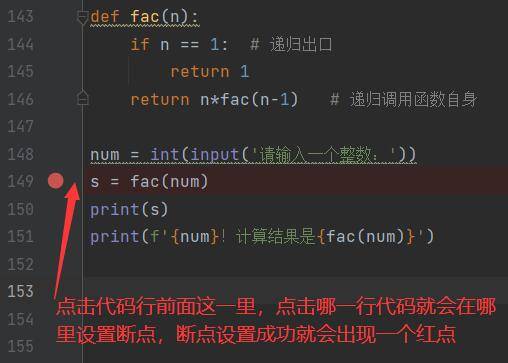
每递归调用一次函数，都会在栈内存分配一个栈帧，每执行完一次函数，都会释放相应的空间。（可以通过pycharm的debug调试去观察这个过程）

示例2：斐波那契数列

# 斐波那契数列  1 1 2 3 5 8 13     第三项等于前两项之和
def fib(n):
    if n < 3:   # 递归出口
        return 1
    return fib(n-2) + fib(n-1)
    # 使用条件表达式：x if 判断条件 else y
    # return 1 if n<3 else  fib(n-2)+fib(n-1)

num = int(input('请输入一个整数：'))
print(f'第{num}个斐波那契数列是{fib(num)}')

# 打印输出前num个斐波那契数列
for i in range(1,num+1):
    print(fib(i),end='\t')

示例3：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。应该如何挪动？

这个问题就是有X、Y、Z三根柱子，将X柱子上的64个圆盘挪到Z柱子上。对于这个问题，可以简单分成三个步骤：

1、将前63个圆盘从 X 移动到 Y 上。

2、将最底下的第64个圆盘从 X 移到 Z 上。

3、再将 Y 上的63个圆盘移到Z上。

那么问题就变成：“如何将 X 上的63个圆盘借助 Z 移动到 Y 上？”和 “如何将 Y 上的63个圆盘借助 X 移到 Z 上“

问题一：“如何将 X 上的63个圆盘借助 Z 移动到 Y 上？”又可以分为三个步骤：

1、将前62个圆盘从 X 移动到 Z 上。

2、将最底下的第63个圆盘从 X 移到 Y 上。

3、将 Z 上的62个圆盘移动到 Y 上。

问题一：“如何将 Y 上的63个圆盘借助 X 移到 Z 上”又可以分为三个步骤：

1、将前62个圆盘从 Y 移动到 X 上。

2、将最底下的第63个圆盘从 Y 移动到 Z 上。

3、将 X 上的62个圆盘移动到 Z 上。

这样看每一个步骤都是一个新的汉诺塔游戏，这样一直分下去，直到n为1，如果只有一个圆盘的话，直接将它从 X 移动到 Z 上即可。

按照递归的思想来看，汉诺塔问题分为三个步骤即可：

1、将前 n-1 个圆盘从 x 移动到 y 上。

2、将最底下的那个圆盘从 x 移动到 z 上。

3、将 y 上的 n-1 个圆盘移动到 z 上。

def hanoi(n,x,y,z): # n个圆盘，x是原柱子，y是过渡柱子，z是目标柱子，xyz是形参
    if n == 1:
        print(x,'--->',z)   # 只有一个圆盘时，直接移动
    else:
        hanoi(n-1,x,z,y)     # 将前n-1个圆盘从x移动到y上
        print(x,'--->',z)    # 将第n个圆盘从x移动z上
        hanoi(n-1,y,x,z)     # 将y上的n-1个圆盘移到z上

num = int(input('请输入汉诺塔的层数：'))

hanoi(num,'X','Y','Z')

递归的优缺点

缺点：占用了大量的内存和时间，效率低。

优点：思路和代码简单，递归可以将复杂的任务分解成一些简单的小问题。

递归函数、函数嵌套和高阶函数的区别

递归函数：在函数体内调用函数本身。

函数嵌套：在一个函数中调用另一个函数。

高阶函数：接收另一个函数作为参数的函数。